QuantMath

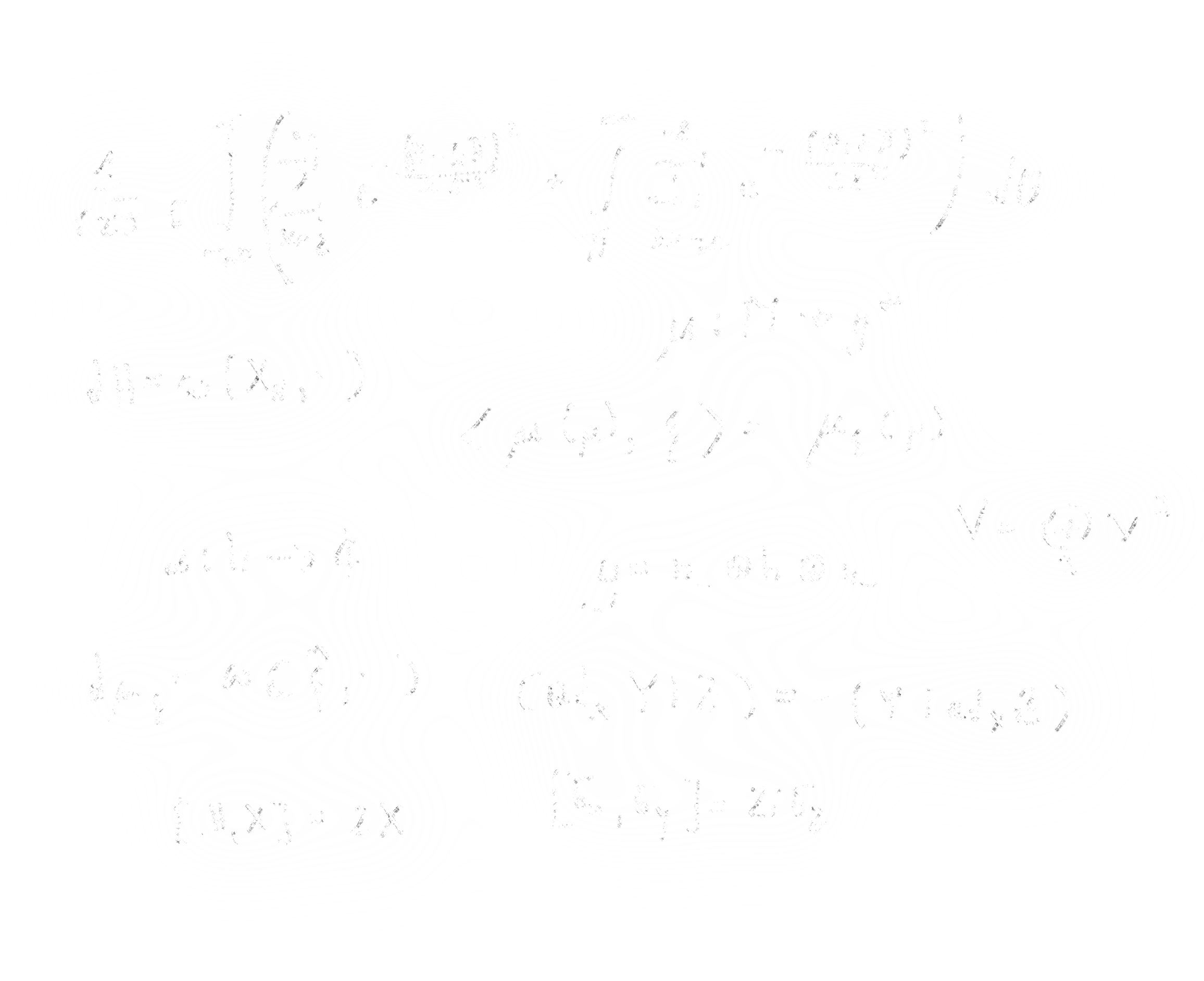
Quantum Mathematics
Research group led by Adam Sawicki

Quantum Information Theory, Quantum Computing, Quantum Graphs, Topology and Geometry in Quantum Mechanics, Configuration Spaces, Anyons, Quantum Statistics

News

Below you will find most important news about our research, activities and community around QuantMath.

10/28/2022

A group member Lorenzo Mattioli defended his PhD thesis! Congratulations!

10/21/2022

What is a relationship between Random Matrix Theory and t-designs made from Haar random gates? This and more in a new preprint:

A random matrix model for approximate t-designs

02/10/2022

How many random gates do we need to construct a t-design? This and more in a new preprint:

Matrix concentration inequalities and efficiency of random universal sets of quantum gates

01/27/2022

How to explicitly bound the efficiency of quantum gates? – new preprint:

Calculable lower bounds on the efficiency of universal sets of quantum gates

12/30/2021

A group member Oskar Słowik defends his MSc thesis in Mathematics!

11/06/2021

Checking universality of quantum gates is now easy! A new preprint:

How to check universality of quantum gates?

01/05/2021 – new publication in Quantum

Designing locally maximally entangled quantum states with arbitrary local symmetries

11/20/2020

Our proposal – Efficient sets of gates and shallow quantum circuits – received funding from NCN in OPUS-19 competition (ST2 panel)!

11/08/2020 – new preprint

A construction for locally maximally entangled states with large symmetries

09/30/2020

A group member Oskar Słowik defends his MSc thesis in Physics!

07/21/2020 – new preprint

Connection between ε-nets and t-designs

07/01/2020

Piotr Dulian joins the group to work on quantum compilation problems.

About the Group

We are keen on all problems that involve quantum theory and interesting mathematics. In particular the group members have worked on:

– description of quantum entanglement in many body systems and quantum marginal problem using symplectic/algebraic geometry and representation theory

– classification of quantum statistics (anyons) on quantum graphs and quantum networks using algebraic topology

– characterisation of isospectral/isoscattering quantum graphs using representation theory of finite groups

– universality of quantum gates using Lie groups theory and number theory

– efficiency of quantum gates using ideas from the theory of random walks on compact groups

– membership problem for quantum gate-sets

Our research is funded by the Center for Theoretical Physics PAS and the National Science Center, Poland through Sonata Bis and Opus grants.